The structured derivation format is a further development of the calculational proofs that were originally proposed by Edsger W. Dijkstra, Wim Feijen, and Nettie van Gasteren, in the 1980s. A calculational proof is essentially a chain of relations, written with explicit justifications for each step in the chain. A calculational proof looks as follows:

The new thing here is that each calculation step comes with an explicit justification. And that the justifications are now considered as first class citizens, getting as much space as the formulas in the derivation. This makes it much easier to read and understand the derivation.
An objection that some have against this format is that the justification is written between the terms in the calculation. This conflicts with their view of what is mathematically pleasing and aesthetic. I had the same problems when I first started to use this formalism. However, this notation grows on you, and after a while, you start to see the beauty of it, and appreciate the added clarity that it brings to a calculation. I am grateful to Edsger Dijkstra, Wim Feijen, Nettie van Gasteren, and, in particular, David Gries, for teaching me to appreciate this notation.
The traditional way of writing calculations does allow to add justifications in the right margin. However, justifications are then seen as just additional comments and not essential parts of the argumentation. In addition, they share the same line with the formula itself, so they are necessarily short. They are not treated as first class citizens. Below we show side by side a standard calculation (without justifications) and a calculational proof. In both cases, the task is to calculate the value of \tan \frac{17\pi}{3}.
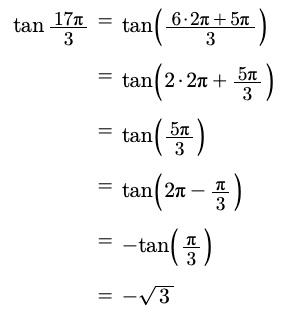

The calculational proof is longer, because it includes all explanations for the step. It is also much easier to read, for the same reason. The difference is well captured in the names: a calculation is just that, mechanically listing successive transformations of an algebraic expression. Whereas a calculational proof is a proof, it also explains why the calculated value is the correct value.
There is now ample space for both terms and for justifications for each step. The proof format forces the user to explicitly write the justifications in the calculation, or otherwise leave ugly empty justification lines. This teaches the basic idea of a proof: each derivation step must be justified. An additional advantage is that it is much easier to check the solution and identify and correct errors in the calculation.
The calculational proof style was developed as part of research into programming methodology, where Dijkstra was one of the central figures. The goal in programming methodology is to write programs that are both efficient and error free. A central idea is to prove mathematically that the program works as required.
Proving the correctness of programs will usually result in a large number of mathematically trivial but sometimes logically complex proofs. Dijkstra’s group developed the calculational proof style as part of their work on how to reason about program correctness in an intuitive way. The calculational proof style became quite popular in the programming methods research community, but was not much spread outside it. A number of textbooks on programming methods and program verification use and propagate this format, like the work by E.W. Dijkstra and C. Scholten, J. van Snepscheut, and D. Gries and F. Schneider. The latter also made a case for using this approach to math teaching, in particular for teaching discrete mathematics at university level.
Structured derivations
Structured derivations is a further development of the calculational style, developed by Joakim von Wright and me. The research has been carried out since the middle of the 1990s We first presented the structured derivation format in our graduate textbook on the foundations of programming methodology, Back & von Wright: Refinement Calculus: A Systematic Introduction, Springer Verlag 1998.
Structured derivations extended the calculational proof style in a number of different ways. It allows for using inference rules in derivations, through the mechanism of nested derivations. It shows how to integrate assumptions and definitions in calculations, as well as traditional conclusion steps. The structured derivation format allows us to construct arbitrary large and complex proofs, while still preserving the main idea of the calculational style, that each derivation step must be explicitly justified.
An important theoretical difference between calculational proofs and structured derivations is that the former is based on a Hilbert like proof system, while structured derivations are based on Gentzen like natural deduction proof systems. A structured derivation is equivalent to a natural deduction proof (in a sequent calculus formulation). However, a structured derivation is much more user friendly than the standard way of expressing a natural deduction proof.
Natural deduction is based on the standard proof techniques developed by mathematicians through the ages. These proof techniques are formulated as inference rules. The natural deduction inference rules are all available in structured derivations. Most mechanised (computer based) proof systems are also based on Gentzen like proof systems. For those who are interested in the fundamentals, the logical bases for structured derivations is described in much more details in this article: “R. – J. Back. Structured derivations: a unified proof style for teaching mathematics. In Formal Aspects of Computing, Springer Verlag, 2009, 22 (5), pp.629-661″. An even more recent presentation is in the book on structured derivations: R. – J. Back: Teaching Mathematics in the Digital Age with Structured Derivations, Four Ferries Publishing, 2015 (available at Amazon).
The structured derivation format unifies the three main proof formats used today in mathematics:
- forward proofs, i.e., classic Euclidean proofs and Hilbert style proofs
- backward proofs, i.e., Gentzen-style natural deduction proofs, and
- calculations, i.e., standard arithmetic and algebraic calculations, as well as calculational proofs.
Any proof in one of these formats can be directly expressed as a structured derivation. Moreover, the overall derivation can be divided into subproblems, which can then be solved using the format that is most appropriate for the task. We can combine forward reasoning, backward reasoning and calculations within a single proof format, structured derivations.
We will illustrate the three proof paradigms by looking at how to prove a simple theorem.
Problem. Prove that k^2+k is even, for any natural number k.
The proof will use the predicates even and odd, with the obvious interpretation. Our first proof will be a standard forward prooff, where the final conclusion is derived through a sequence of intermediate steps. Each conclusion step follows from the assumptions or the preceding conclusion steps.
A traditional forward proof
A forward proof starts by listing the assumptions, and then deducing the required conclusion by a sequence of intermediate conclusion steps. Here we first declare that the variable k is an integer, and assume that it is a non-negative integer. We then proceed with a sequence of conclusion steps, until we get the conclusion that we are looking for, and the theorem is proved.

A calculational proof
We start with the same assumptions. But then we prove the theorem by showing that it is equivalent to T (the logical constant true), which is the same as saying that the property is true. The symbol \vee stands for logical “or”.

A backward proof
The backward proof will reduce the original problem to two simpler problems with a case analysis: proving that the property holds when k is even, and that it also holds when k is odd. The two cases are given as nested derivations for the top-level justification of the theorem. The two cases are then assumed to hold by the justifications given.

Combining forward, backward and calculational proofs
Our last proof shows how to combine all these three proof methods in a single structured derivation. The derivation starts as the others, with the declaration and assumption. Then comes a conclusion step that shows how to rewrite the original expression.We prove the theorem with case analysis, as above. But this time we show for each case that it is true with a calculation.
Notice the use of backward implication in one of the steps, in both cases. Backward implication is sufficient, because it is sufficient to show that the theorem follows from T (the logical constant “true”).
