Structured derivations is the underlying format for writing mathematical derivations in eMath Studio. We give here an overview of the format, and then describe typical ways in which the format is used.
The main principles behind structured derivations are the following:
- The way we write a derivation should be close to standard mathematical practice
- The description of a derivtion should be transparent, i.e., contain all information that is needed to understand the derivation
- The derivation should show explicitly the logical structure of the argument
- The derivation should be precise enough so that a computer can check whether it is correct
Some of these requirements are in conflict with each other. Standard mathematical practice is not precise enough for a computer to understand it, and certainly not to be able to check the mathematical correctness of the argument. Also, standard practice requires a lot of the logical argument to be expressed in prose, thus hiding the overall structure of the argument.
On the other hand, earlier attempts at creating a mathematical notation that is understandable for a computer have often resulted in a language that is far away from the way most mathematicians work, and in particular far away from how mathematics is taught in schools today. These formats (known as interactive theorem provers and automatic theorem provers) have advanced the techniques for proving mathematics with a computer and the understanding of mathematical proofs tremendously, but their use require highly skilled mathematics and computer science professionals.
Structured derivations attempt at striking middle ground between the two extremes: a language for writing mathemtical arguments (derivations) that is precise enough so that the argument can be checked for correctness by a computer, but close enough to standard mathematical notation that it can be used in math education, from middle and high school level up to university level mathematics.
Advantages of structured derivations
Structured derivations is a language for writing mathematical derivations and proofs (a proof language), that comes with its own editor (eMath Editor) and own correctness checker (eMath Checker). We summarise here the main advantages of using structured derivations for writing mathematical arguments.
The main advantages of structured derivations as a proof language are listed below:
- Structured derivations provide a fixed format for structuring mathematical derivations and proofs that can be used for any kinds of mathematical argumentation
- The format teaches the idea of a proof by insisting that each derivation step is justified and by providing a standard template for how to write the justifications.
- A structured derivation shows explicitly the structure of the logical argumentation (hence the name structured derivations).
Because of the fixed format, a structured derivation can be supported by computers. An editor for structured derivation provides additional advantages:
- An editor can check that the syntax of a structured derivation is correct, and supports the user in constructing a structured derivation (syntax directed editing).
- An editor allows the user to modify the derivation as the solution proceeds, reflecting increased understanding of the problem and the solution.
- The derivation is much easier to read and communicate when it is created by an editor.
- An editor can provide an outlining facility that allows the structured derivation to be studied at different levels of detail, either focusing on the overall structure of the argument, or looking closely at some details in the argumentation.
The fact that a structured derivations have an exact logical meaning comes with an added, very important advantage: The correctness of a structured derivation can be checked by a computer:
- The computer can check each step in the derivation, and mark all the steps that it can prove correct.
- If all steps in the derivation are proved correct, then the derivation as a whole is mathematically correct.
- Steps that are not proved correct are either wrong, or the proof was too difficult to find, or there some information that the computer needed to prove the step was missing.
In this way, the computer will show the user which derivation steps require attention, either to fix the bug, help the computer finding a proof by giving a more detailed derivation, or by adding information that the computer needs to find a proof.
Example of structured derivation
A structured derivation at the top level is just a sequence of context items. A context item is either a (variable or constant) declaration, a definition, an assumption, a conclusion, a calculation, or a task. We give here an example of a structured derivation. The derivation solves the following word problem:
The grandfather is 40 year older than the grandson. After 4 years, the grandfather will be twice as old as the grandson. How old are the grandfather and the grandson?
Here is the structured derivation that solves this problem. We have here indicated explicitly the kind of each context item, on the left.

The derivation starts by declaring two variables, s\in \mathbb{R} (the grandson’s age) and f\in \mathbb{R} (the grandfather’s age).Both these are real valued variables, as indicated by their type \mathbb{R} . The declaration is followed by a comment that explains what these variables stand for in the problem formulation.
Then we have to assumptions, f=s+40 and f+4=2(s+4), which are again explained by comments.
Finally, the problem is solved in two conclusion steps. The first one calculates the value of s from the equation, s=36, and the second gives the answer, s=36\land f=76. The way we solve the equation is hidden in this derivation (the three dots \ldots indicate that there is hidden content for the first conclusion step).
This example shows a derivation with three different context items: declarations, assumptions, and conclusion steps. In general, a derivation can consist of any of the above mentioned context items, in any order. Each context item provides some information that can used by later context items in the derivation.
Context items
Let us explain the role of the different context items in somewhat more detail.
Variable declaration. A variable declaration introduces new names that are used as variables in the derivation. The declaration lists the names of the variables and their value range. For instance, x,y,z\in \mathbb{R} says that we now can use variables named x,y,z in the derivation, and that these variables range over real numbers. The standard value ranges (types) are \mathbb{R} for real numbers, \mathbb{Z} for integers, and \mathbb{B} for truth values.
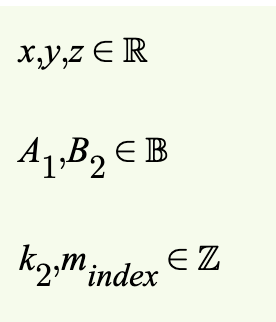
Constant declaration. A constant declaration introduces a name for a constant and gives it a value. For instance, c=23.4 introduces a constant called c that has the value 23.4 (a real number). The value of a constant can be a numeric or logical constant, or an expression that refers to previously defined constants and variables.
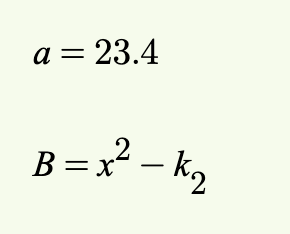
Definition. A definition is another way of introducing a constant. It is used mostly for defining functions. For instance, f:A\to B defines a new function f with domain A and codomain B. The definition specifies the value of the function on a separate line, here f(x)=x^2 +2. The justification explains why the function is well-defined (but is not really needed for explicit function definitions like here).

Assumption An assumption states a property of the declared variables and constants that we are allowed to assume in the sequel. For instance, the assumption could be that x+y= a
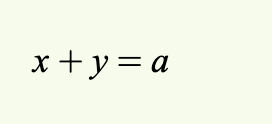
Conclusion step A conclusion step shows a property (a logical expression) that follows from the previous context. The justification explains why this property is true in the context of previous assumptions, definitions, constan declarations, and conclusion steps.
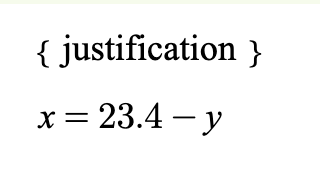
Calculation A calculation is a sequence of expressions with a relation between each expression. The calculation is used to derive a relationsship between the first expression and the last one. The justification for each step explains why the relation between the terms is true. The first justification in the example on the right would explain why x = a-y , and the second justification would explain why a-y= 23.4-y

Task A task is used when we want to explicitly state the problem to be solved and the answer for the problem. The problem is stated after the bullet, and the answer is stated after the square. Tasks are, e.g., used for formulating theorems and for dividing a larger problem into smaller problems. The justification explains why the answer is correct.

Justifications
Each logical step in a structured derivation comes with a justification, written inside curly brackets. The justification for a conclusion step explains why the conclusion follows from the preceeding context, the justification for a calculation step explains why the indicated relation holds between the two expressions, and the justification for the task explains why the answer is correct.
Sometimes a simple textual justification inside curly brackets is not enough, the step requires a more careful explanation. This is done by giving supporting arguments for the step in the form of nested derivations. A nested derivation is written under the justification, and is indented to the right. A nested derivation can be either a calculation or a task. A justification can have zero or more nested derivations.
The example that we looked at above had a hidden nested derivation, the calculation that shows how we solved the equation. The complete derivation is shown here below.

Different views
The eMath editor allows us to view structured derivations in different ways. We can have a view that shows the kind of each context item, as we show above (the Types view). We can have a view that uses keywords instead of explicit types, like this.

We can also have a very simple view, which just shows numbers for the steps (the default view), as follows:
