Proofs are of central importance for understanding mathematics, any deeper understanding of mathematics require that you know how to read proofs and how to construct proofs yourself. But writing proofs is seen as difficult in (Finnish) high school math today, and is usually avoided. The same is true in other countries as well. Students are not taught how to write proofs. The few proofs that are given are intuitive and informal, and varying in style and rigour. The best students will still pick up the basic idea of doing mathematics: to derive a result by a sequence of well-justified steps. The rest will see mathematics as just a collection of templates to memorise, solving problems with these without any deeper understanding.
Avoiding proofs means that the students are given a very shallow understanding of mathematics. The argument for avoiding proofs is that it is too difficult for students to understand. On the other hand, not doing proofs will also make mathematics difficult to understand. The way we write proofs has a long tradition and has not essentially changed since it was first introduced by Euclides in Elements, his treatment of contemporary mathematics, written around 300 BC. This way of doing mathematics has been the guiding principle for mathematicians through the ages.
A solution to this dilemma may lay in making proofs themselves easier to understand, so that they can be taught at middle and high school level. This is the main idea behind structured derivations. This is a language for writing mathematical derivations that require (i) that each step in the derivation comes with an explicit justification, and (ii) that the structure of a derivation shows the logical structure of the argument.
On justifications
A proof is essentially a sequence of conclusion steps starting from a given set of assumptions. Each conclusion step has to be explicitly justified. The justifications are written so that the person who writes the proof can check that the argumentation is correct. They are also written to communicate the proof to others, to help them understand the argumentation and check it for themselves, to see whether they agree with it or not.
Students in schools are usually not used to justifying their argumentation. A solution to an exercises is given as a sequence of calculation steps, without justifying the individual steps. The important thing is to get the right answer. However, in real life, there is no one to tell you what is the right answer. The reason that you do the calculation is exactly because you don’t know the right answer. The only way to be certain of the result is to carefully check and justify each step.
We exemplify the need for justifications with a problem taken from trigonometry. We choose a slightly more complicated derivation, in order to show the difficulties in following a mathematical argument without explicit justifications. This puts the reader in a similar position as, say, a middle school student who tries to understand a derivation with fractions for the first time.
Problem. Calculate the value \tan \frac{17\pi}{3}.
Solution. The teacher shows the following solution on the whiteboard:
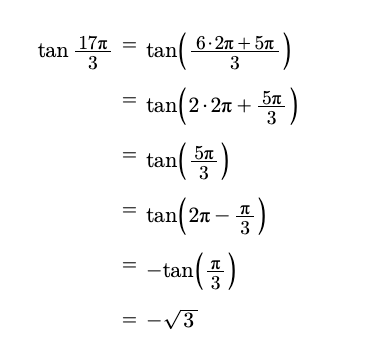
The teacher has written all the formulas on the whiteboard, but explains each step only verbally. However, the verbal explanations are lost for many students, because
- the student was stuck on understanding some step, and could not follow the remaining steps,
- the student was thinking about something else, and was not paying attention,
- the student was not even attending the class, or
- any number of other reasons.
What remains is the derivation written on the whiteboard.
Doing homework. At home, the student works on homework assignments. For this, he/she needs to understand the example that the teacher presented during lecture. If the student was not able to follow and understand the verbal explanations, he/she now has to decipher this derivation and find out the justification for each step. This is an error prone process, involving a lot of guesswork, trial and error, and so on.
For those who persist and are strongly motivated, this is actually not that bad as teaching method. They learn to understand the theory behind the calculation, and gain a deeper understanding. Essentially, they will recreate the proof of the calculation, for themselves. These students go on to become good at mathematics, with many continuing their studies in STEM subjects with a solid understanding of mathematics.
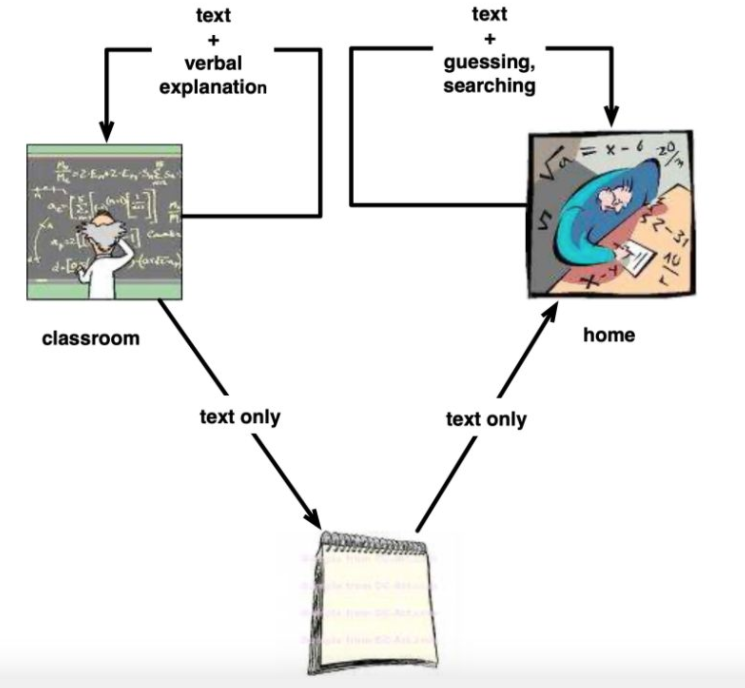
However, this method does not work that well for students with less strong motivations. They might not even try to understand the derivation, or then they will guess the reasons for the different steps, without deeper understanding. Wrong guesses will lead to problems of understanding later on, in other math courses. The errors and missunderstandings accumulate for the student for each course, until the going becomes too difficult and the student gives up. They find mathematics too difficult, and will self-identify as bad in mathematics. The situation is illustrated in the figure below.
This situation could be acceptable, if teaching mathematics was just some kind of competition with the purpose of identifying the best math students and promoting their careers. But this is not the situation today. Our highly technical societies need many more people skilled in mathematics than what the education system is delivering today. And everybody should have a basic understanding of mathematics. In ancient times, reading and writing was in a similar situation. There were special clerks and monks who mastered writing, and they took care of the needs of the society. But nowadays this would not be sufficient. Reading and writing is a skill that everybody needs to master, at least at some basic level.
The real tragedy here is that we are essentially dealing with a communication problem. The teacher has the information about why each step is justified, and the teacher also communicates this information, during class. But this information is lost on the way to the student, because there is no standard and agreed way of including this information in the written presentation. Verbal communication is not sufficient, the justifications need to be an integral part of the derivation.
The question now is how to write the justification as part of the calculation. A solution to this problem was developed by Edsger Dijkstra, Wim Feijen, and Nettie van Gasteren in the 1980s, known as a calculational proof. A calculational proof is essentially a chain of relations of the form
where \simis a binary transitive relation on some domain.
Structured derivations is a further development of the calculational proof format, where we have added the possibility of defining the context of the calculation (what variables are used, constant and function definitions, and assumptions), as well as support for standard mathematical inference rules (as nested derivations), forward and backward proofs, and expressing theorems (known as tasks).
A calculational proof / structured derivation expresses the above relation chain as follows:

The new thing here is that each calculation step comes with an explicit justification. And that the justifications are now considered as first class citizens, getting as much space as the formulas in the derivation. This makes it much easier to read and understand the derivation.
The traditional way of writing calculations does allow for adding justifications, in the right margin. However, the justifications are then seen as just additional comments, they share the same line with the formula itself, so they are necessarily short. They are not treated as first class citizens.
Let us now show how the above calculation can be written as a calculational proof / structured derivation.

There is now ample space for both terms and for justifications for each step. The proof format forces the teacher to write the justifications explicitly, not just stating them verbally. And it forces the students to write their justifications also for each step. This teaches the student the idea of a proof: each derivation step must be justified.
An additional advantage is that the student can check the solution much more easy for themselves, and identify and correct errors in their calculation. The format makes it also easier for the teacher to identify what a student has and has not understood, and to check the correctness of the student’s solution.
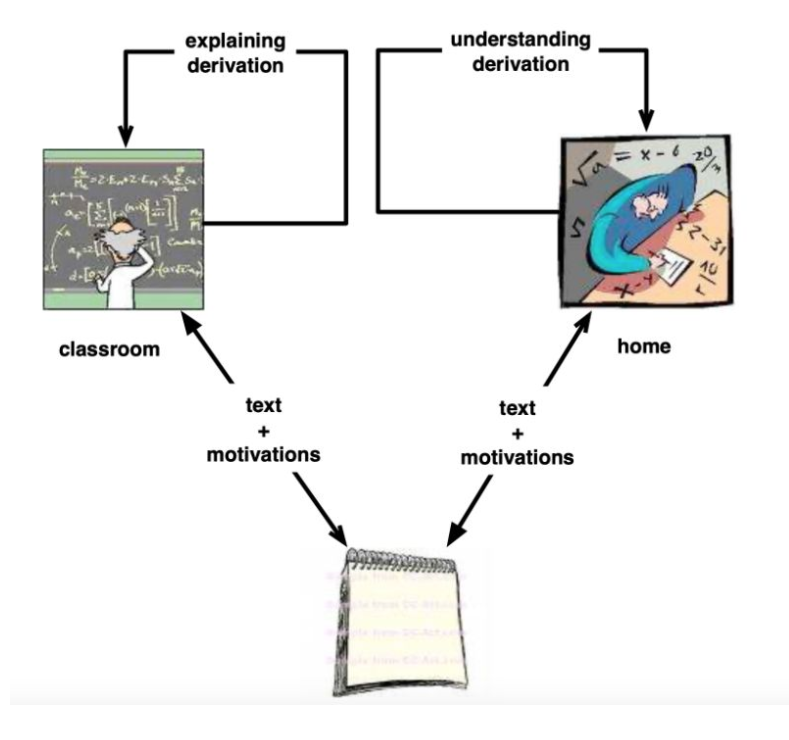
The figure below shows how calculational proofs improve on the learning situation, when both the calculation and the motivation for each step (the justification) is communicated to the student.